全微分 偏微分 偏导数

08 Jun 2020

1. 偏微分

对于一元函数，微分即是切线；

对于多元函数，可以想象为三维空间的一条曲线，其实这个空间曲线是这个空间平面与这个空间曲面的交线.

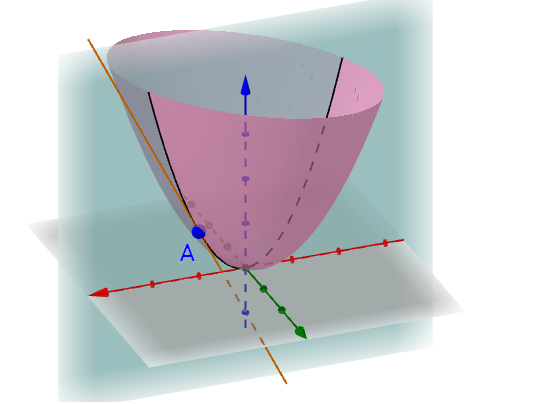
这个切线称为\(f(x,y)\)对于的偏微分。为什么是对于的呢？因为这是与的交线，在这条线上无论点怎么变化，都要满足，即是常数不会变化。

举一反三：

对于所有的曲面，偏微分都可以看作是y=C与\(f(x,y)\)的交线上点的切线，所以是\(f(x,y)\)对于x的偏微分。

2. 偏导数

偏微分的斜率。

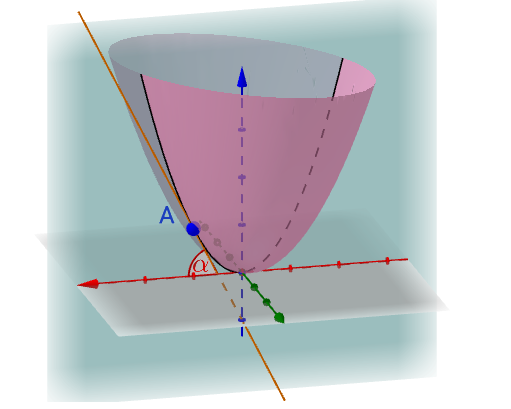
3. 全微分

如果这些平面与函数的交线的切线都存在，并且这些切线（无数条）还都在同一个平面上（平面不是曲面），那么得到的这个平面就是全微分（也叫做切平面，或者说切空间）

4. 彼此的关系

根据全微分的定义，如果全微分存在，那么偏导数、偏微分一定存在。

但是反过来不一定成立，即偏导数、偏微分存在，全微分不一定存在。因为偏导、偏微分只是x或y方向的导数和微分，而全微分要求360°无死角。

举个例子，看这个\(f(x,y)= \frac{x y}{\sqrt{x^2+y^2}}\)

{\displaystyle \scriptstyle (x_{0}+\Delta x,\ y_{0}+\Delta y)} 为该邻域内的任意一点，则该函数在点{\displaystyle (x_{0},\ y_{0})}的變化量 {\displaystyle \scriptstyle \Delta f=f(x_{0}+\Delta x,\ y_{0}+\Delta y)-f(x_{0},\ y_{0})} 可表示为

参考：https://www.matongxue.com/madocs/219.html