反向传播
1. Introduction
反向传播的核心是对代价函数 \(C\) 关于 \(w\) (或者 \(b\))的偏导数 \(\partial C/\partial w\) 的计算表示。该表示告诉我们在权重和偏差发生改变时,代价函数变化的快慢。
2. 损失函数/代价函数的组成
我们使用 \(w_{jk}^l\) 表示从 \((l-1)^{th}\) 层的 \(k^{th}\) 个神经元到 \((l)^{th}\) 层的 \(j^{th}\) 个神经元的链接上的权重,\(b_J^l\) 表示在 \(l^{th}\) 层 \(j^{th}\) 个神经元的偏差,使用 \(a_j^l\) 表示 \(l^{th}\) 层 \(j^{th}\) 个神经元的激活值。下面的图清楚地解释了这样表示的含义:
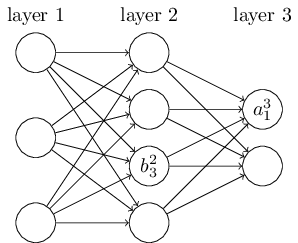
有了这些表示, \(l^{th}\) 层的 \(j^{th}\) 个神经元的激活值 \(a_j^l\) 就和 \(l^{th}\) 层关联起来了(对比公式(4) 和上一章的讨论)
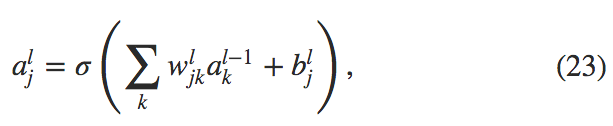
也可以使用向量的形式写成:

这个表达式给出了一种更加全局的思考每层的激活值和前一层的关联方式:我们仅仅用权重矩阵作用在激活值上,然后加上一个偏差向量,最后作用 \(\sigma\) 函数。
3. 两个假设
二次代价函数有下列形式:
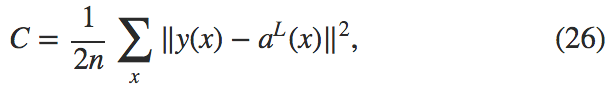
其中 \(n\) 是训练样本的总数;求和是在所有的训练样本 \(x\) 上进行的;\(y = y(x)\) 是对应的目标输出;\(L\) 表示网络的层数;\(a^L = a^L(x)\) 是当输入是 \(x\) 时的网络输出的激活值向量。
3.1 假设1:代价函数可以被写成一个 在每个训练样本 \(x\) 上的代价函数 \(C_x\) 的均值
\[C=\frac{1}{n} \sum_x C_x\]| 对每个独立的训练样本其代价是:$$C_x = \frac{1}{2} | y-a^L | ^2$$ |
要这个假设的原因是反向传播实际上是对一个独立的训练样本计算了 \(\partial C_x/\partial w\) 和 \(\partial C_x/\partial b\)。然后我们通过在所有训练样本上进行平均化获得 \(\partial C/\partial w\) 和 \(\partial C/\partial b\)。实际上,有了这个假设,我们会认为训练样本 \(x\) 已经被固定住了,丢掉了其下标,将代价函数 \(C_x\) 看做 \(C\)。
3.2 假设2:代价可以写成神经网络输出的函数
例如,二次代价函数满足这个要求,因为对于一个单独的训练样本 \(x\) 其二次代价函数可以写作:
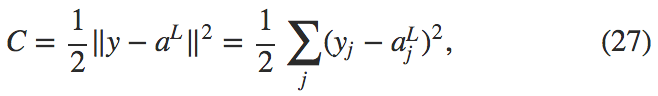
这是输出的激活值的函数。当然,这个代价函数同样还依赖于目标输出 \(y\)。记住,输入的训练样本 \(x\) 是固定的,所以输出同样是一个固定的参数。所以说,并不是可以随意改变权重和偏差的,也就是说,这不是神经网络学习的对象。所以,将 \(C\) 看成仅有输出激活值 \(a^L\) 的函数才是合理的,而 \(y\) 仅仅是帮助定义函数的参数而已。
4. 反向传播的四个基本方程
Hadamard 乘积
反向传播算法基于常规的线性代数运算——诸如向量加法,向量矩阵乘法等。但是有一个运算不大常见。特别地,假设 \(s\)和 \(t\) 是两个同样维度的向量。那么我们使用 \(s\odot t\) 来表示按元素的乘积。所以 \(s\odot t\) 的元素就是 \((s\odot t)_j = s_j t_j\)。给个例子,

这种类型的按元素乘法有时候被称为 Hadamard 乘积或者 Schur 乘积。我们这里取前者。好的矩阵库通常会提供 Hadamard 乘积的快速实现,在实现反向传播的时候用起来很方便。
4.1 输出层误差
假定存在一个很小的扰动 \(\Delta z_j^l\) 在神经元的带权输入上,使得神经元输出由 \(\sigma(z_j^l)\) 变成 \(\sigma(z_j^l + \Delta z_j^l)\)。这个变化会向网络后面的层进行传播,最终导致整个代价函数产生 \(\frac{\partial C}{\partial z_j^l} \Delta z_j^l\) 的改变。我们定义 \(l\) 层的第 \(j^{th}\) 个神经元上的误差 \(\delta_j^l\) 为:

输出层误差的方程,\(\delta^L\):每个元素定义如下:

这是一个非常自然的表达式。右式第一个项 \(\partial C/\partial a_j^L\) 表示代价随着 \(j^{th}\) 输出激活值的变化而变化的速度。假如 \(C\) 不太依赖一个特定的输出神经元 \(j\),那么\(\delta_j^L\) 就会很小,这也是我们想要的效果。右式第二项 \(\sigma'(z_j^L)\) 刻画了在 \(z_j^L\) 处激活函数 \(\sigma\) 变化的速度。
注意到在 BP1 中的每个部分都是很好计算的。特别地,我们在前向传播计算网络行为时已经计算过 \(z_j^L\),这仅仅需要一点点额外工作就可以计算 \(\sigma'(z_j^L)\)。当然 \(\partial C/\partial a_j^L\) 依赖于代价函数的形式。然而,给定了代价函数,计算\(\partial C/\partial a_j^L\)就没有什么大问题了。例如,如果我们使用二次函数,那么 \(C = \frac{1}{2} \sum_j(y_j-a_j)^2\),所以 \(\partial C/\partial a_j^L = (a_j - y_j)\),这其实很容易计算。
方程(BP1)对 \(\delta^L\) 来说是个按部分构成的表达式。这是一个非常好的表达式,但不是我们期望的用矩阵表示的形式。但是,重写方程其实很简单,

这里 \(\nabla_a C\) 被定义成一个向量,其元素师偏导数 \(\partial C/\partial a_j^L\)。你可以将其看成 \(C\) 关于输出激活值的改变速度。方程(BP1)和方程(BP1a)的等价也是显而易见的,所以现在开始,我们会交替地使用这两个方程。举个例子,在二次代价函数时,我们有 \(\nabla_a C = (a^L - y)\),所以(BP1)的整个矩阵形式就变成
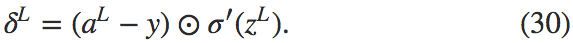
如你所见,这个方程中的每个项都有一个很好的向量形式,所以也可以很方便地使用像 Numpy 这样的矩阵库进行计算了。
4.2 下一层误差
使用下一层的误差 \(\delta^{l+1}\) 来表示当前层的误差 \(\delta_l\):特别地,

其中 \((w^{l+1})^T\) 是 \((l+1)^{th}\) 权重矩阵 \(w^{l+1}\) 的转置。这其实可以很直觉地看做是后在 \(l^{th}\) 层的输出的误差的反向传播,给出了某种关于误差的度量方式。然后,我们进行 Hadamard 乘积运算 \(\odot \sigma'(z^l)\)。这会让误差通过 \(l\) 层的激活函数反向传递回来并给出在第 \(l\) 层的带权输入的误差 \(\delta\)。
通过组合(BP1)和(BP2),我们可以计算任何层的误差了。首先使用(BP1)计算\(\delta^l\),然后应用方程(BP2)来计算\(\delta^{L-1}\),然后不断作用(BP2),一步一步地反向传播完整个网络。
4.3 代价函数关于偏置的改变率

这其实是,误差 \(\delta_j^l\) 和偏导数值 \(\partial C/\partial b_j^l\)完全一致。这是很好的性质,因为(BP1)和(BP2)已经告诉我们如何计算 \(\delta_j^l\)。所以就可以将(BP3)简记为

其中 \(\delta\) 和偏差 \(b\) 都是针对同一个神经元。
4.4 代价函数关于权重的改变率

这告诉我们如何计算偏导数 \(\partial C/\partial w_{jk}^l\),其中 \(\delta^l\) \(a^{l-1}\) 这些量我们都已经知道如何计算了。方程也可以写成下面少下标的表示:

其中 \(a_{in}\) 是输出给 \(w\) 产生的神经元的输入和 \(\delta_{out}\)是来自 \(w\) 的神经元输出的误差。放大看看权重 w,还有两个由这个链接相连的神经元,我们给出一幅图如下:

方程(32)的一个结论就是当激活值很小,梯度 \(\partial C/\partial w\) 也会变得很小。这样,我们就说权重学习缓慢,表示在梯度下降的时候,这个权重不会改变太多。换言之,(BP4)的后果就是来自很低的激活值神经元的权重学习会非常缓慢。

5. 反向传播算法
5.1 链式求导
链式法则:
\[(f(g(x)))'=f'(g(x))*g'(x))\]将链式法则应用与神经网络梯度计算,自然而然就会得到上式这种反式微分,所以叫反向传播。
由于符号微分的出现:即给定一个运算链,并且已知每个运算的导数,这些框架就可以利用链式法则来计算这个运算链的梯度函数
反向传播方程给出了一种计算代价函数梯度的方法。让我们显式地用算法描述出来:
- 输入 \(x\):为输入层设置对应的激活值 \(a^l\) 。
- 前向传播:对每个 \(l=2,3,...,L\) 计算相应的 \(z^l = w^la^{l-1} + b^l\) 和 \(a^l = \sigma(z^l)\)
- 输出层误差 \(\delta^L\):计算向量 \(\delta^L = \nabla_a C \odot \sigma'(z^L)\)
- 反向误差传播:对每个 \(l=L-1, L-2,...,2\),计算 \(\delta^l = ((w^{l+1})^T\delta^{l+1})\odot \sigma'(z^l)\)
- 输出:代价函数的梯度由 \(\frac{C}{w_{jk}^l} = a_k^{l-1}\delta_j^j\) 和 \(\frac{\partial C}{\partial b_j^l} = \delta_j^l\)
看看这个算法,你可以看到为何它被称作反向传播。我们从最后一层开始向后计算误差向量 \(\delta^l\)。这看起来有点奇怪,为何要从后面开始。但是如果你认真思考反向传播的证明,这种反向移动其实是代价函数是网络输出的函数的后果。为了理解代价随前面层的权重和偏差变化的规律,我们需要重复作用链式法则,反向地获得需要的表达式。