梯度为0

08 Jun 2020

1. Hessian矩阵

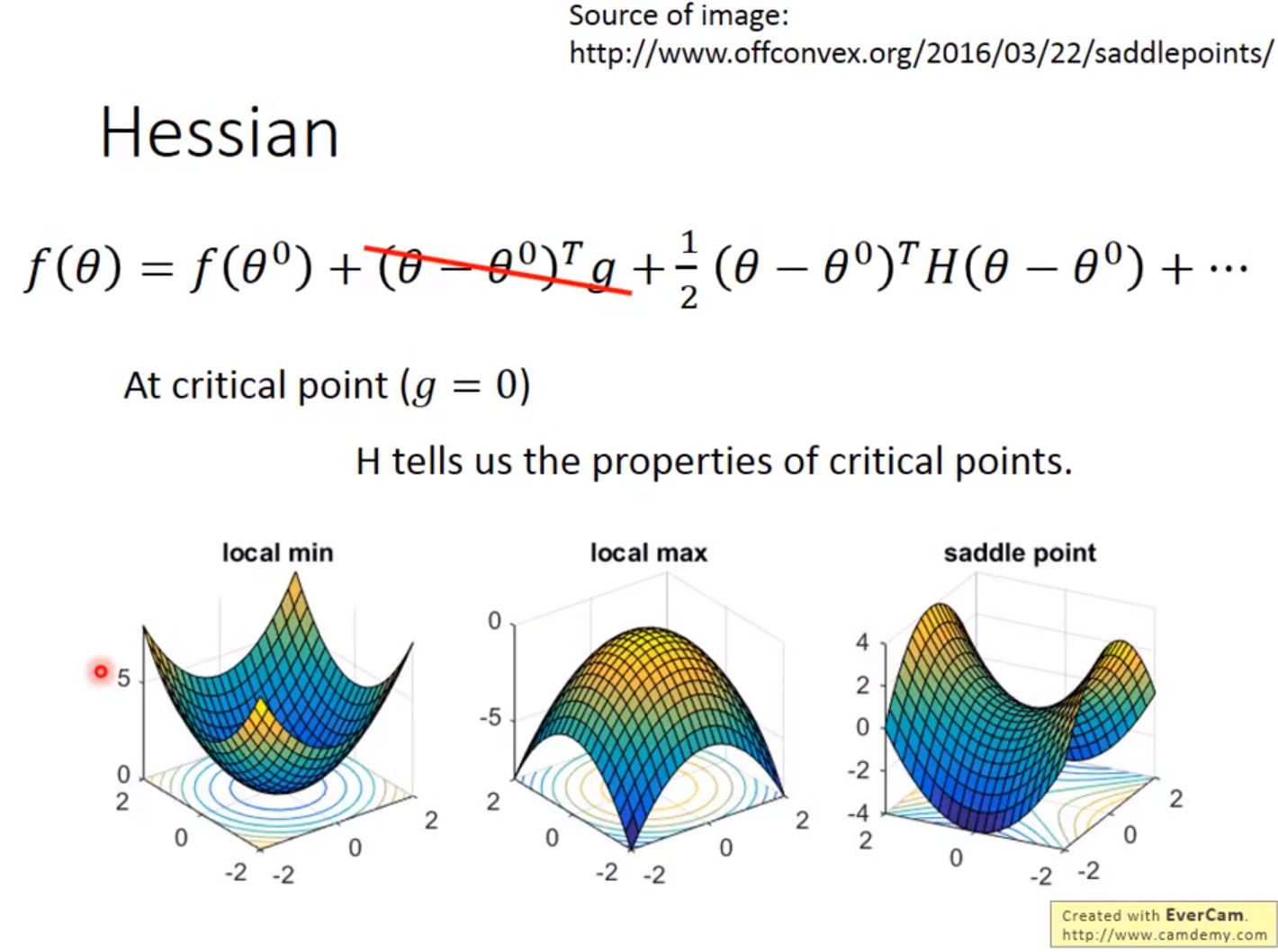
用泰勒展开对loss函数展开：第一项为常量、第二项为一次导数、第三项为二次倒数（偏微分中组成hessian矩阵。

如果一次倒数为0，那么$f(\theta)$由hessian决定；

一次倒数为0有如下三种情况；极大值位置、极小值位置、鞍点（saddle point）

image-20200514143939028

2. 特征向量与特征值

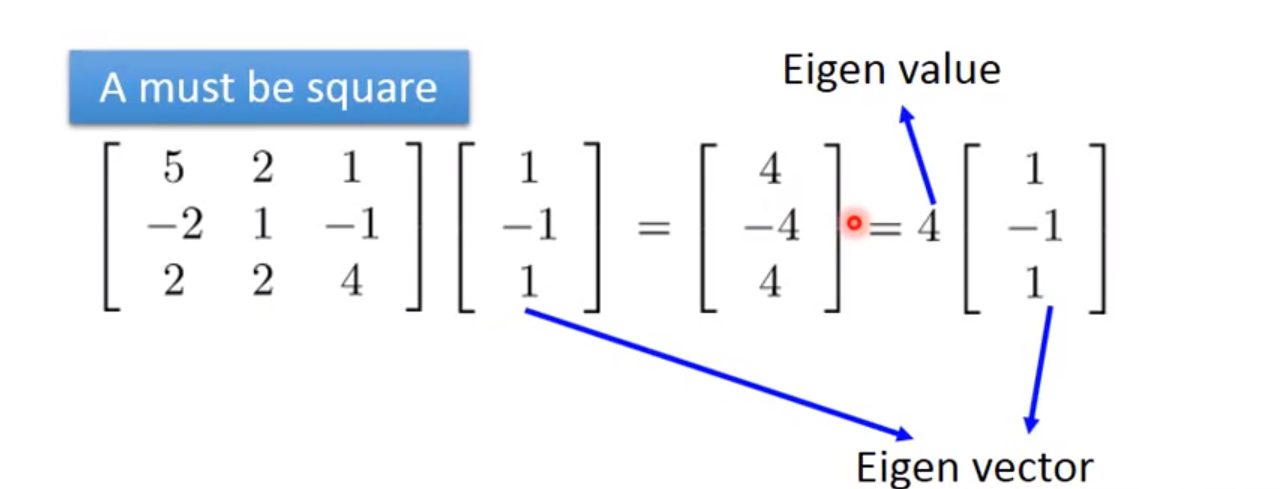
image-20200514144221272

2.1 正定矩阵

一个n×n的实对称矩阵{\displaystyle M}M是正定的，当且仅当对于所有的非零实系数向量z，都有$z^TMz > 0$。其中zT表示z的转置，z是非零的。

3. 极值

image-20200514145006750

当$xHx\le 0$；那么$f(\theta)$与$f(\theta……0)$的关系由后面的$O(\theta^3)$项决定

4. 海塞矩阵特征值

image-20200514150029576

image-20200514161449584

Hessian矩阵的特征值就是复形容其在该点附近特征向量方向的凹凸性，特征值越大，凸性越强，它控制着步长。

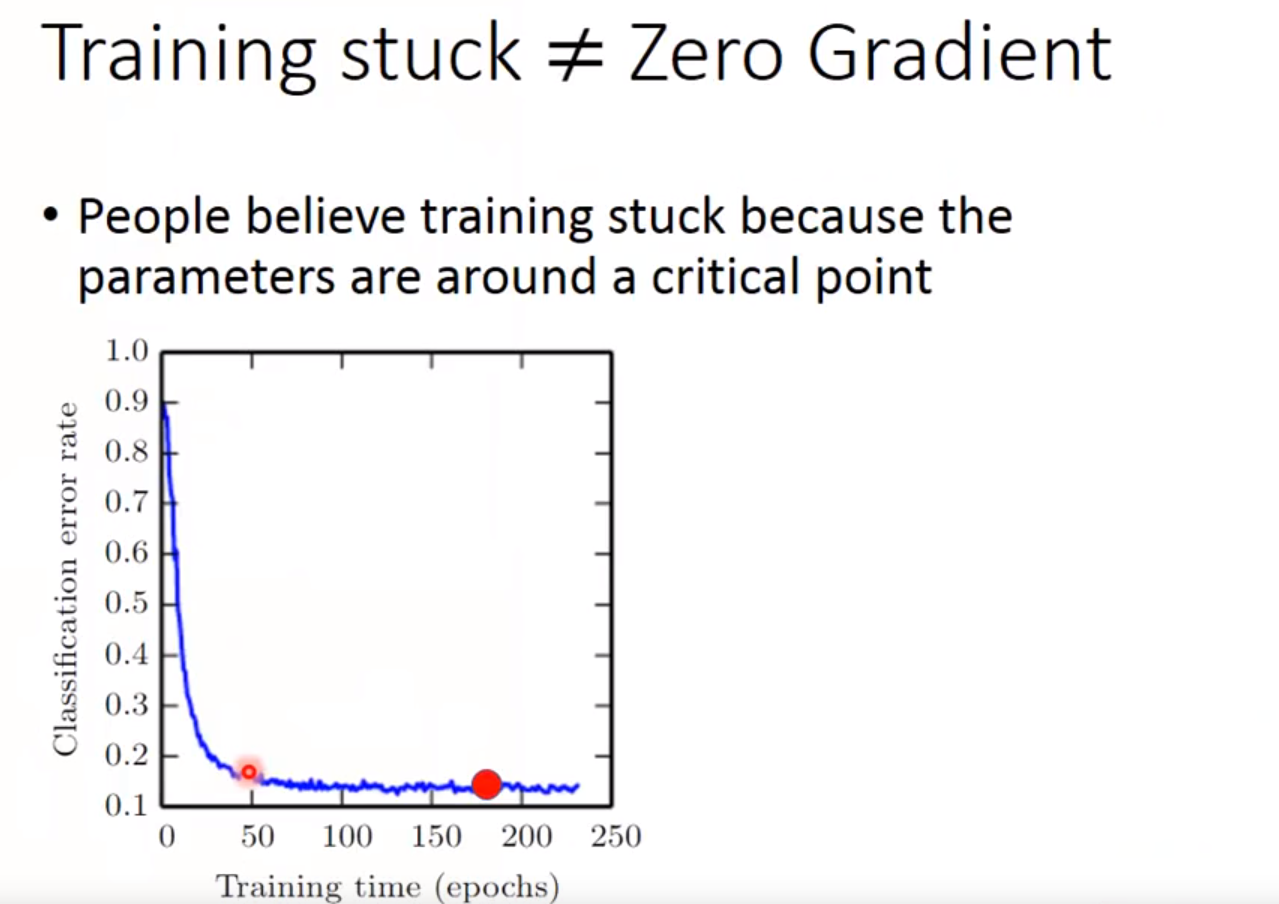
image-20200514150442715

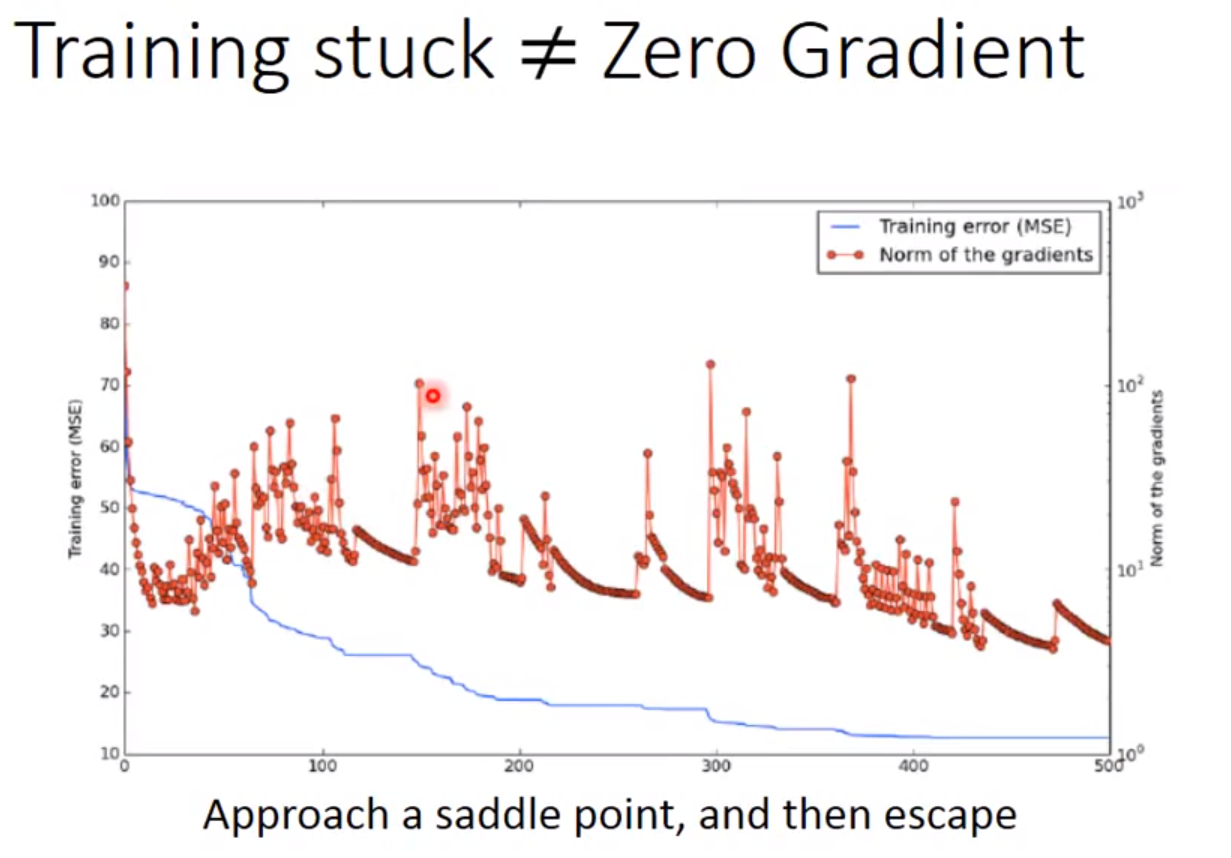
image-20200514150540756

### 局部最小都是全局最小？？